UTS

1.        Jelaskan secara singkat apa yang dimaksud dengan Jaringan Syaraf Tiruan (JST)!

Jawaban: Jaringan Syaraf Tiruan (JST) merupakan salah satu representasi buatan dari otak manusia yang selalu mencoba untuk mensimulasikan proses pembelajaran pada otak manusia tersebut. Istilah buatan di sini digunakan karena jaringan syaraf ini diimplementasikan dengan menggunakan program komputer yang mampu menyelesaikan sejumlah proses perhitungan selama proses pembelajaran.

2.        Jelaskan tentang proses perceptron!

Jawaban: Perceptron biasanya digunakan untuk mengklasifikasikan suatu tipe pola tertentu yang sering dikenal dengan pemisahan secara linear. Pada dasarnya, perceptron pada jaringan syaraf dengan satu lapisan memiliki bobot yang bisa diatur dan suatu nilai ambang (threshold). Algoritma yang digunakan oleh aturan perceptron ini akan mengatur parameter-parameter bebasnya melalui proses pembelajaran. Nilai threshold (q) pada fungsi aktivasi adalan non negatif. Fungsi aktivasi ini dibuat sedemikian rupa sehingga terjadi pembatasan antara daerah positif dan daerah negatif (Gambar 1.1).

Gambar 1.1 Pembatasan linear dengan perceptron

Garis pemisah antara daerah positif dan daerah nol memiliki pertidaksamaan:

Sedangkan garis pemisah antara negatif dengan daerah nol memiliki pertidaksamaan:

Misalkan kita gunakan pasangan vektor input s dan vektor output sebagai pasangan vektor yang akan dilatih.

Algoritma:

a.       Inisialisasi semua bobot dan bias:

(untuk sederhananya set semua bobot dan bobot bias sama dengan nol).

Set learning rate: a (0 < a £ 1).
(untuk sederhananya set sama dengan 1).

b.      Selama kondisi berhenti bernilai false, lakukan langkah-langkah sebagai
berikut:

·         Untuk setiap pasangan pembelajaran s-t, kerjakan:

-      Set input dengan nilai sama dengan vektor input:

-      Hitung respon untuk unit output:

-      Perbaiki bobot dan bias jika terjadi error:

Jika y ¹ t maka:

wi(baru) = wi(lama) + a*t*xi

b(baru) = b(lama) + a*t

jika tidak, maka:

wi(baru) = wi(lama)

b(baru) = b(lama)

·         Tes kondisi berhenti: jika tidak terjadi perubahan bobot pada (i) maka kondisi berhenti TRUE, namun jika masih terjadi perubahan maka kondisi berhenti FALSE.

Algoritma di atas bisa digunakan baik untuk input biner maupun bipolar, dengan q tertentu, dan bias yang dapat diatur. Pada algoritma tersebut bobot-bobot yang diperbaiki hanyalah bobot-bobot yang berhubungan dengan input yang aktif (xi ¹ 0) dan bobot-bobot yang tidak menghasilkan nilai y yang benar.

3.        Jelaskan tentang proses madaline!

Jawaban: Madaline (Many Adaline) adalah ekstensi multilayer dari single-neuron bipolar Adaline ke suatu jaringan. Struktur dasar dari Madaline ini dapat dilihat pada gambar 5.1, dan gambar 5.2 memperlihatkan Madaline yang terdiri dari dua layers Adaline, ditambah sebuah layers input yang hanya berfungsi sebagai distributor input jaringan.

Gambar 5.1 A simple Madaline structure

Gambar 5.2 The Madaline network of 2 layers

Madaline Training

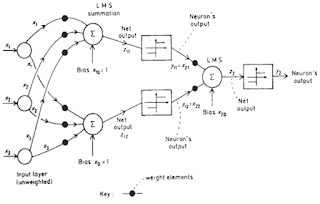
Dalam Madaline terdapat sebuah layer tersembunyi. Gambar 5.3 menunjukkan arsitektur Madaline untuk 2 buah masukan x1 dan x2, sebuah layer tersembunyi yang terdiri dari 2 unit neuron tersembunyi z1 dan z2, dan sebuah keluaran Y.

Gambar 5.3

Keluaran dari unit tersembunyi z1 dan z2 adalah nilai fungsi aktivasi yang diterima dari x1 dan x2. Demikian pula unit keluaran Y merupakan nilai fungsi aktivasi dari z1 dan z2. Meskipun keluaran z1 dan z2 masing-masing merupakan fungsi linier, tetapi keluaran Y bukanlah fungsi linier x1 dan x2 karena adanya unit tersembunyi.

Algoritma pelatihan Madaline II adalah sebagai berikut:

1.         Inisialisasi bobot

·           v₁=1/2, v₂=1/2, b₃=1/2

·           bobot yang lain menggunakan bilangan random yang kecil

·           nilai learning rate ditentukan antara 0,1 ≤ na ≤ 1.0

2.         Untuk setiap bipolar input pada vektor x

·           Set aktivasi dari input unit ke x

·           Hitung masukan jaringan ke setiap hidden unit

Zin₁ = b₁ + x₁w₁₁ + x₂w₂₁

Zin₂ = b₂ + x₁w₁₂ + x₂w₂₁

·           Tentukan output dari setiap hidden unit

Z₁ = f(Zin_i)

Z₂ = f(Zin_i)

3.         Untuk setiap bipolar input pada vektor x

·           Tentukan keluaran dari jaringan

Yin = b₃ + z₁v₁ +z₂v₂

Y = f(Yin)

·           Hitung error dan update bobot, jika t≠y maka laukan update bobot untuk setiap hidden unit dengan input mendekati 0

-          Ubah keluaran unit (dari +1 menjadi –1, atau sebaliknya)

-          Hitung kembali respon dari jaringan. Jika kesalahan berkurang: Sesuaikan bobot pada unit ini (gunakan nilai keluaran yang baru sebagai target dan lakukan aturan Delta)

bj (new) = bj (old) + ∝ (1 – zinj)
wij (new) = wij (old) + ∝ (1 – zinj) xi
bk (new) = bk (old) + ∝ (-1 – zink)
wik (new) = wik (old) + ∝ (-1 – zink) xi

4.        Jelaskan secara singkat proses aplikasi memakai metode back propagation tentang character recognition!

Jawaban:

a.      Pengenalan

Permasalahan yang akan dipecahkan kali ini adalah masalah pengenalan karakter sederhana menggunakan jaringan perceptrons dengan prosedur pembelajaran back propagation. Tugas kita adalah mengajarkan jaringan saraf untuk mengenali 3 karakter, yaitu, untuk memetakan mereka untuk masing-masing pasangan {0,1}, {1,0} dan {1,1}. Dan diharapkan jaringan menghasilkan sinyal error {0,0} dalam menanggapi karakter lain.

b.      Desain Jaringan

-          Struktur

Jaringan saraf dari desain ini terdiri dari tiga lapisan dengan 2 neuron masing-masing, satu lapisan output dan dua lapisan tersembunyi. Ada 36 masukan ke jaringan. Dalam kasus ini fungsi sigmoid:

dipilih sebagai fungsi aktivasi neuron nonlinear. hal Bias (sama dengan 1) dengan bobot dilatih juga dimasukkan dalam struktur jaringan. Diagram struktural dari jaringan saraf yang diberikan pada Gambar. 6.A.1.

-          Desain Database

Kami mengajarkan jaringan saraf untuk mengenali karakter 'A', 'B' dan 'C'. Untuk melatih jaringan untuk menghasilkan sinyal kesalahan kita akan menggunakan 'D' lain 6 karakter, 'E', 'F', 'G', 'H' dan 'I'. Untuk memeriksa apakah jaringan telah belajar untuk mengenali kesalahan kita akan menggunakan karakter 'X', 'Y' dan 'Z'. Perhatikan bahwa kami tertarik dalam memeriksa respon dari jaringan untuk kesalahan pada karakter yang tidak terlibat dalam prosedur pelatihan.

Karakter untuk diakui diberikan pada 6 × 6 kotak. Masing-masing dari 36 piksel diatur ke 0 atau 1. Sesuai 6 × 6 matriks dari representasi karakter diberikan sebagai:

-          Set-up jaringan

Algoritma pembelajaran Kembali propagasi (BP) dari Bagian 6.2 digunakan untuk memecahkan masalah. Tujuan dari algoritma ini adalah untuk meminimalkan kesalahan-energi pada lapisan output, seperti dalam Sect. 6.2 di atas, menggunakan persamaan (6.17), (6.19), (6.26), (6.27) daripadanya. Dalam metode ini satu set pelatihan vektor input diterapkan vektor-by-vektor ke input dari jaringan dan maju-disebarkan ke output. Bobot kemudian disesuaikan dengan algoritma BP seperti di atas. Selanjutnya, kita ulangi langkah ini untuk semua set pelatihan. Seluruh proses ini kemudian diulang untuk selanjutnya (m + 2) iterasi -th dan sebagainya. Kami berhenti ketika konvergensi memadai tercapai.

Kode program di C ++ ditulis untuk mensimulasikan respon dari jaringan dan melakukan prosedur pembelajaran, seperti di Bagian 6.A.5 bawah.

c.       Hasil

-          Pelatihan jaringan

Untuk melatih jaringan untuk mengenali karakter di atas kita diterapkan sesuai 6 × 6 grid dalam bentuk 1 × 36 vektor ke input dari jaringan. Karakter dianggap diakui jika kedua output dari jaringan yang tidak lebih dari 0,1 off nilai-nilai yang diinginkan masing-masing. Awal tingkat belajar η adalah eksperimental diatur ke 1,5 dan menurun dengan faktor 2 setelah setiap iterasi 100. Pendekatan ini, bagaimanapun, menghasilkan prosedur pembelajaran terjebak dalam berbagai minima lokal. Kami mencoba menjalankan algoritma belajar untuk 1000 iterasi dan menjadi jelas bahwa parameter kesalahan-energi telah berkumpul untuk beberapa nilai stabil, namun pengakuan gagal untuk semua karakter (vektor).

Namun, tak satu pun dari vektor pelatihan kami diakui pada saat ini:

Pelatihan vektor 0, 1, ..., 8 di entri log ini sesuai dengan karakter 'A', 'B',. . . , 'I'.

Untuk mencegah hal ini terjadi, satu lagi modifikasi dibuat. Setelah setiap iterasi 400 kita ulang tingkat belajar nilai awalnya. Kemudian setelah sekitar 2000 iterasi kami mampu konvergen ke 0 kesalahan dan untuk benar mengenali semua karakter:

-          Hasil pengenalan

Dalam rangka untuk menentukan apakah kesalahan deteksi dilakukan dengan benar, kita diselamatkan bobot yang diperoleh ke dalam file data, memodifikasi dataset dalam program menggantikan karakter 'G', 'H' dan 'I' (pelatihan vektor 6, 7 dan 8) dengan karakter 'X', 'Y' dan 'Z'. Kami kemudian berlari program, dimuat bobot disimpan sebelumnya dari file data dan diterapkan input ke jaringan. Perhatikan bahwa kami melakukan pelatihan lebih lanjut. Kami mendapat hasil sebagai berikut:

Semua tiga karakter yang berhasil dipetakan kesalahan sinyal 0,0.

-          Robustness Investigation

Untuk menyelidiki bagaimana kuat jaringan syaraf kami, kami menambahkan beberapa kebisingan untuk input dan mendapat hasil berikut. Dalam kasus 1-bit distorsi (dari 36 bit) tingkat pengakuan adalah:

Kami juga menyelidiki kasus 2-bit distorsi dan mampu mencapai tingkat pengakuan berikut:

d.      Diskusi dan kesimpulan

Kami mampu untuk melatih jaringan saraf kita sehingga berhasil eecognizes tiga karakter yang diberikan dan pada saat yang sama mampu mengklasifikasikan karakter lain sebagai kesalahan. Namun, ada harga yang harus dibayar untuk kenyamanan ini. Tampaknya bahwa semakin besar tingkat deteksi kesalahan adalah, kurang kuat jaringan kami adalah. Misalnya, ketika 2 bit karakter 'A' yang terdistorsi, jaringan memiliki tingkat pengenalan hanya 53%. Secara kasar, pada 1 dari 2 kasus tersebut, jaringan 'berpikir' bahwa input tidak simbol 'A' dan karena itu harus diklasifikasikan sebagai kesalahan. Secara keseluruhan, jaringan propagasi kembali terbukti menjadi jauh lebih kuat daripada Madaline. Hal ini dimungkinkan untuk mencapai konvergensi lebih cepat dan juga lebih mudah untuk program ini. Ada kasus, namun, ketika algoritma pembelajaran propagasi kembali terjebak dalam minimum lokal tetapi mereka dapat berhasil ditangani oleh tuning tingkat pembelajaran dan hukum mengubah tingkat belajar selama proses pembelajaran untuk setiap masalah khusus.

5.        Berikan suatu contoh aplikasi JST berikut beserta penjelasannya!

Jawaban: 

Jaringan Syaraf Tiruan untuk Klasifikasi Citra Daun

1. Latar Belakang
2. Rumusan Masalah
3. Tujuan Penelitian
4. Tinjauan Pustaka
5. Metode Penelitian
6. Kesimpulan

[Kembali]