7.5. Network Stability
Penyesuaian
berat dalam jaringan umpan balik harus menjamin stabilitas jaringan. ditunjukkan
oleh Cohen dan Grossberg (1983) bahwa jaringan berulang dapat dijamin stabil
jika matriks W bobot simetris dan jika diagonal nol, yaitu
Persyaratan
di atas hasil dari Lyapunov stabilitas teorema yang menyatakan bahwa sistem
(jaringan) stabil jika fungsi energi (fungsi Lyapunov nya) dapat didefinisikan
untuk sistem yang yang dijamin untuk selalu menurun dari waktu ke waktu
[Lyapunov, 1907, lihat juga Sage dan Putih, 1977]. Jaringan (atau sistem)
stabilitas dapat terpenuhi melalui Lyapunov stabilitas teorema jika fungsi E
dari y dari jaringan (sistem), lihat kondisi berikut:
Kondisi
(A): Setiap perubahan y dari jaringan (sistem) hasil penurunan E.
Kondisi
(B): E dibatasi dari bawah.
Dengan
demikian energi E (dilambangkan juga sebagai fungsi Lyapunov) sebagai berikut :
j
yang menunjukkan neuron j
Ij
berada di masukan eksternal untuk neuron j
Thj
menjadi ambang untuk neuron j
wij
menjadi sebuah elemen dari matriks bobot W, untuk menunjukkan berat dari output
dari
neuron i ke input dari neuron j.
Kami
sekarang membuktikan stabilitas jaringan dengan teorema Lyapunov sebagai
berikut: Pertama kami menetapkan W menjadi simetris dengan semua elemen
diagonal menjadi nol, yaitu
membuktikan
bahwa kondisi E terpenuhi (A) dari Lyapunov stabilitas teorema, oleh mempertimbangkan perubahan dan hanya dalam
satu komponen yk (n + 1) dari lapisan output:
Yang
menunjukkan E (n) sebagai E pada iterasi n dan yk(n) sebagai yk
pada saat itu iterasi yang sama, ditulis:
where
dan
di mana Thk menunjukkan untuk diberikan (kth) neuron. Oleh karena
itu, yk dapat melakukan dua perubahan nilai:
However, this can occur only if
oleh Persamaan. (7.26) di atas. Oleh karena itu, oleh Persamaan. (7.25) ∆E <0, sehingga E berkurang sebagai yang dibutuhkan oleh kondisi (A) dari teorema Lyapunov Stabilitas. Demikian pula dalam skenario (ii);
oleh Persamaan. (7.26) di atas. Oleh karena itu, oleh Persamaan. (7.25) ∆E <0, sehingga E berkurang sebagai yang dibutuhkan oleh kondisi (A) dari teorema Lyapunov Stabilitas. Demikian pula dalam skenario (ii);
oleh
Persamaan. (7.26) di atas. Oleh karena itu, sekali lagi ∆E <0 sehingga E ini
direduksi kembali seperti yang diperlukan. Akhirnya, kondisi (B) dari Lyapunov
stabilitas. dalam kasus terburuk (kasus yang paling negatif energi) semua yi
= yj = 1 sehingga


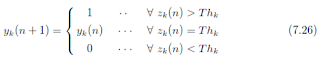




Komentar
Posting Komentar