BAB 4

4.1. The Basic Structure

Perceptron adalah salah satu metode JST training yang sederhana dipakaikan prosedur algoritma training yang pertama kali. Terdiri dari neuron tunggal dengan bobot synaptic yang diatur menggunakan fungsi aktifasi hard limit.

4.1       Dasar Struktur

Perceptron berfungsi sebagai sebuah blok bangunan untuk sebagian besar model .,termasuk Adaline seperti yg dibahas sebelumnya yang Model neuron mungkin dianggap sebagai kasus khusus dari Perceptron. The Perceptrron memiliki satu struktur dasar seperti pada Gambar. 

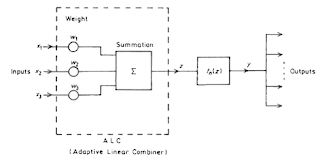
Gambar 4.1 Struktur dasar jaringan saraf tiruan

              

            Struktur pada gambar diatas adalah bentuk standar satuan unit jaringan otak manusia yang telah disederhanakan. Jaringan otak manusia tersusun tidak kurang dari 10¹³ buah neuron yang masing-masing terhubung oleh sekitar 10¹⁵ buah dendrite. Fungsi dendrite adalah sebagai penyampai sinyal dari neuron tersebut ke neouron yang terhubung dengannya. Sebagai keluaran, setiap neuron memiliki axon, sedangkan sebagai penerima sinyal disebut synapse. 

Gambar 4.2 Perceptron (Saraf Tiruan)

Fungsi keluaran dari perceptron adalan sebagai berikut: 

Dimana,

T merupakan nilai transpos dari W

4.1.1. Fungsi aktivasi perceptron

Fungsi aktifasi f(zi), dimana fungsi nonlinier yang menghasilkan keluaran:

Sehingga,

Atau fungsi aktifasi yang lain:

Dimana fungsi ini menyerupai persamaan 4.6 dengan:

Fungsi aktifasi sederhana dari hard limit dirumuskan sebagai berikut :

Dalam banyak aplikasi fungsi aplikasi dipindahkan sehingga output y berkisar antara -1 hingga +1. 

Sehingga melalui persamaan 4.6,

Atau melalui persamaan 4.7:

4.2. The Single-Layer Representation Problem

Teorema pembelajaran perceptron dirumuskan oleh Rosenblatt pada tahun 1961. teorema perceptron dapat belajar (memecahkan) apa pun dapat mewakili (Mensimulasikan). Namun, kita akan melihat bahwa teorema ini tidak berlaku untuk satu Perceptron (atau untuk setiap model neuronal dengan output biner atau bipolar, seperti di Bab 3) atau untuk satu lapisan model neuron tersebut. Kita akan lihat nanti bahwa itu tidak berlaku untuk model di mana neuron yang terhubung dalam jaringan multi-layer. Perceptron single layer menghasilkan deskripsi representasi untuk situasi dua input. representasi ini berlaku untuk beberapa neuron tersebut dalam lapisan tunggal jika mereka tidak interkoneksi. Dengan teorema representasi, perceptron dapat 
menyelesaikan semua masalah yang atau dapat direduksi menjadi masalah pemisahan linier (klasifikasi).

4.3. The Limitations of the Single-Layer Perceptron

Pada tahun 1969, Minsky dan Papert menerbitkan sebuah buku di mana mereka menunjukkan seperti yang dilakukan E. B. Derek pada tahun 1965 dalam sebuah buku yang kurang dikenal, dengan keterbatasan dalam kemampuan dari perceptron, seperti terbukti dengan teorema perwakilannya. Mereka telah menunjukkan bahwa, misalnya, perceptron tidak bisa memecahkan Or (XOR) Masalah [(x1 ∪ x2) ∩ (X1 ∪ X2)], atau pelengkap nya, kontradiksi masalah 2-state (XNOR).


Pada single-layer pengklasifikasi tidak bisa memecahkan. Begitu banyak sehingga, bahwa untuk satu lapisan jaringan saraf dengan peningkatan jumlah input, jumlah masalah yang dapat diklasifikasikan menjadi sebagian kecildari totalitas masalah yang dapat dirumuskan. Secara khusus, neuron dengan input biner dapat memiliki pola masukan 2n yang berbeda.Karena setiap pola input dapat menghasilkan 2 output biner yang berbeda, maka ada 22nfungsi yang berbeda dari n variabel. Jumlah masalah yang terpisah secara linear dari n input biner Namun sebagian kecil dari 22 n. 

4.4. Many-Layer Perceptrons

Untuk mengatasi keterbatasan ditunjukkan oleh Minsky dan Papert, Minsky dan Papert (1969) telah menunjukkan bahwa satu-layer ANN dapat memecahkan (mewakili) masalah klasifikasi titik yang terletak di daerah terbuka cembung atau cembung daerah tertutup( wilayah cembung adalah salah satu di mana dua titik dalam daerah dapat dihubungkan dengan garis lurus yang terletak sepenuhnya di daerah itu). Pada tahun 1969 ada tidak ada metode untuk mengatur bobot selain untuk neuron yang output (y) dapat diakses Itu kemudian ditampilkan [Rumelhart et al., 1986] bahwa 2-layer ANN dapat memecahkan juga masalah non-cembung, termasuk masalah XOR atas. Ekstensi untuk tiga atau lebih lapisan meluas kelas masalah yang dapat diwakili dan karenanya diselesaikan dengan ANN untuk, pada dasarnya, tidak ada terikat. Namun, pada 1960-an dan 1970-an ada tidak ada alat yangampuh untuk mengatur bobot dari multi-layer ANN. Meskipun pelatihan multilayer sudah digunakan sampai batas tertentu untuk Madaline, itu lambat dan tidak ketat cukup untuk umum masalah multi-layer.